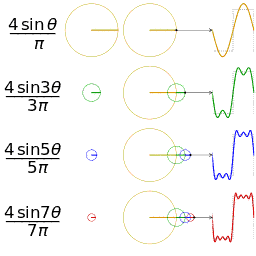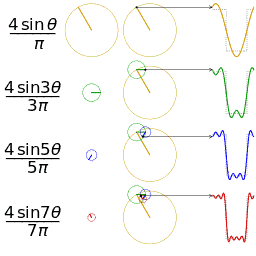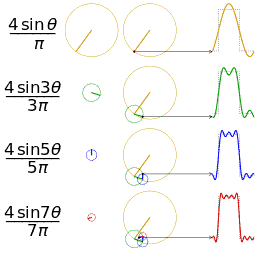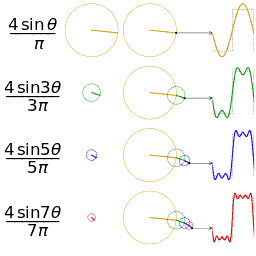I N F O R M A T I O N
Fourier Transforms
French mathematician Joseph Fourier introduced the Fourier Series in 1807, and today the Fourier transform is used a wide variety of applications and nearly all electronic communication.
The basic premise is that every function can be written as an infinite sum of sines and cosines with varying frequencies and amplitudes.
The section on Fourier Analysis in Steven J. Luck's An Introduction to the Event-related Potential Technique (Pg. 18-19) is a good introduction. The Wikipedia page on Fourier Series is another good introduction.
The Fourier transform of a function is plotted with the frequencies in Hertz on the x-axis and the amplitude (or power, which is amplitude squared) of the sine function on the y-axis.
Figure 1: Fourier approximation of a square wave

Figure 2: Fourier series of an ERP
The key thing to understand is that if there is a peak in the power spectrum at a value (such as 48 Hz in Figure 2) there isn't necessarily a physiological or other source producing a perfect sine wave at 48 Hz. Rather, that sine wave is necessary for accurately approximating the waveform of the irregularly shaped ERP.
References
Figure 1: "Fourier series square wave circles animation" by Cmglee - Own work. Licensed under CC BY-SA 3.0 via Wikimedia Commons -https://commons.wikimedia.org/wiki/File:Fourier_series_square_wave_circles_animation.
gif#/media/File:Fourier_series_square_wave_circles_animation.gif