Step 6: Analyze
- Jun 4, 2023
- 8 min read
The analysis process may seem complicated at first, but do not despair! With practice you will soon become a pro at it.
Before beginning the process of analysis, it is important to remind yourself about the all-important effect size. This effect size is the number that you will use to represent the findings from your meta-analysis. It indicates both the magnitude and the direction of your findings.
There are 7 major components to analysis:
(Click on a component for more information)
Step 1: Choosing an effect size statistic
When choosing an effect size statistic, the first aspect to consider is whether your data is standardized or unstandardized. The answer to this question is determined primarily by the method(s) of measurement each study uses to report the variable of interest. If all the data is reported using the same scale, then you can use the unstandardized formulas. However, if you need to compare data across scales (for example, if some studies report depression levels based on a therapist's diagnosis, and others use a self-reported questionnaire) your effect size calculation must be standardized to account for these differences.
Once you have decided if your data needs to be standardized or can remain unstandardized, you must choose which model best represents the effect sizes produced by your study's designs. There are a total of seven options, but keep in mind that you must use the same effect size statistic for your entire data set. This page will discuss the two most common statistics for two-variable relationships.
Pre-Post Contrasts (Mean Gain):
This effect size statistic is selected if the variable of interest is primarily being compared across time to examine change. Studies will report the same variable, measured in the same way, at two or more time points. Studies that should be analyzed using the Mean-Gain model do not require a control group because the participants' baseline values function as their own control.
Example: Does eating a high carbohydrate meal affect FMD? In this case, the primary variable of interest is the participant's FMD before and after carbohydrate ingestion. The comparison occurs between the pre- and post- meal values.
Group Contrasts (Mean Difference):
Select this effect size statistic if your variable of interest is measured on two or more groups and compared across groups. The need to compare an experimental group to a control group is typically an indicator that the Mean Difference model should be used. This effect size statistic can even be used for studies that follow a specific variable across time IF the change in that variable for group 1 is being compared to the change in the same variable for group 2.
Example: Does exercise decrease depression levels? In this case, the variable of interest is participants' depression levels, but in order to understand if exercise has a beneficial effect on depression, the exercise group's results MUST be compared to the results of a control group.
If your data does not fit either of these models, please consult Chapter 3 in Practical Meta-Analysis by Lipsey and Wilson for more information.
Step 2: Computing the effect size and other numbers
Whichever effect size statistic you end up choosing, there are specific formulas used in meta-analysis to calculate (1) effect size, (2) standard error, and (3) the inverse variance (w). You will need to calculate each of these numbers for each effect in your data set. The best way to do this is to enter the equations in Microsoft Excel and then copy&paste or drag the formula down the entire column.
The equations are as follows:

For more information on the variables in these equations, click HERE.
Step 3: Adding in codes for each moderator
In order to successfully accomplish steps 4-7, it is important to carefully complete this step of adding in codes for each moderator. Some of your moderators may already be in code-form thanks to the completion of the coding process. However, you must now assign codes for those moderators that were previously entered into your data set as the raw data.
For example, age, which you most likely entered into the data set as the mean of participants for each effect, can be coded into intervals of 10 years so that every effect with a mean age between 10 and 20 years gets coded as the same number, etc. As you read in the section on how to develop a coding scheme, the codes assigned to each category are arbitrary as long as your research team agrees on them. Essentially, these codes will be used in the following steps to divide your data and analyze it in SPSS by moderator category.
It is a good idea to wait and not add these codes into your spreadsheet until you have downloaded your data into SPSS. To learn how you can easily create a column of codes in SPSS, click HERE and watch the "Contrast Weights and Codes" video.
Step 4: Running MeanES
MeanES is the first of the SPSS macros you will be using. Briefly, a macro is a list of code that automatically performs a specific function each time you run it.
This specific macro will soon become your best friend in the analysis process. MeanES calculates the average effect size of all the selected effects each time you run it. You will be using the values from this macro to create graphs of your moderators by selecting all the effects with a specific characteristic, running MeanEs, and recording the value the macro produces, before repeating the process with a new group of studies. It is important to record the confidence intervals, standard error, and K (number of effects) that the macro will produce as well.
For example, using SPSS capabilities explained HERE, you will run MeanES on all the studies with normal weight participants, then select only those with overweight participants to run the macro on, and finally run it on the studies with obese participants. These results will tell you the differences (or lack thereof) in the effects of BMI on your variable of interest.
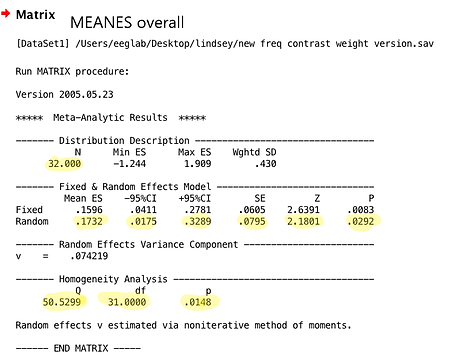
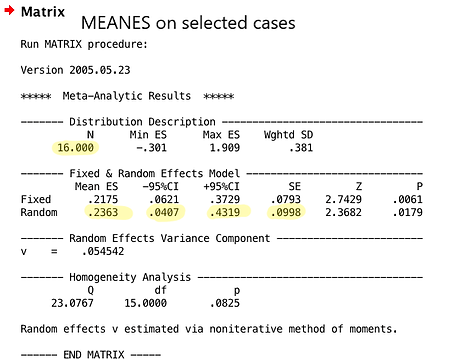
First, The MeanES macro should first be run on all cases to get the overall effect size. Then, the macro should be ran on selected cases to calculate the mean effect size for each category for each moderator. Examples of the output from the MeanES macro for all cases and selected cases, respectively, are shown below. The highlighted values are the numbers that you need.
Step 5: Graphing your results
Once you have the average effect sizes for your various moderators, you can begin graphing. This is an extremely rewarding phase of the meta-analyis process because you finally get to see a product from all your hours of reading and coding. The best tool to use for making quick and helpful graphs is Excel. Make sure that you clearly label each graph and its axes so as to avoid confusion later on.
Once you are ready to create your final graphs, however, SigmaPlot is the way to go. Excel requires that you average your standard error across the categories in your graph, whereas SigmaPlot allows you to customize error bars. In addition, SigmaPlot has the capability to create Forrest plots, a meta-analysis-specific type of graph. Click HERE for tutorials on how to use SigmaPlot.
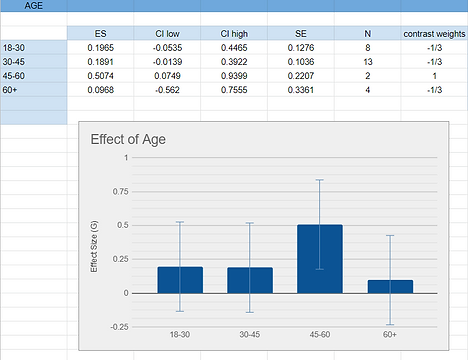
Below is an example of a graph using excel or google sheets (contrast weights which is discussed in the next step are already included in this screenshot).
Step 6: Assigning contrast weights
In order to assign contrast weights, you must first complete your graphs. Then, you will need to decide which moderators to add into the overall meta-regression as factors that potentially explain a part of the variance found between effect sizes. Once you have compiled these graphs, you may start assigning contrast weights. These weights should be entered into your SPSS spreadsheet in a column next to their corresponding code column.
The concept of contrast weights is a somewhat technical and confusing aspect of meta-analysis. However, the basics are fairly easy to understand. Essentially, these weights are necessary because they tell the meta-regression macro how to interpret the moderators and factor their influence into the overall model. One set of contrast weights should correspond to each of your moderators. In a set, the weights must sum to zero, and cannot be greater than 1 or less than -1. A contrast weight of zero essentially tells the meta-regression to ignore all effects with that particular weight. In addition, the sign of the contrast weight does not necessarily need to correspond with the sign of the effect size it is representing. For example, if the effect of carbohydrate ingestion on men versus women is -2.05 and -0.20 respectively, the contrast weight for women would be +1 and -1 for men because the weights are describing the two groups in relation to each other.
Step 7: Running the meta-regression
Running the meta-regression and the univariate analysis are the final steps in the analysis process. The macro used is the MetaReg macro. This macro is run in a similar way to the MeanES macro (Click HERE for an explanation). However, they produce different levels of information. This macro takes the contrast weights into account. Therefore, you should put new variables in the spreadsheet for each moderator and the corresponding contrast weight for that study. If that study is not included in any classfication for the moderator (i.e. does not have a contrast weight) make sure to leave that cell blank. Call this new variable variable_cw (such as bmi_cw if bmi was the moderator). When calling this macro there are a few more variables than the MeanES variable that need to be defined. IVS is either one or a list of "variable_cw". If you are running it on multiple moderators, put spaces between the name. Another variable is the model. The model you should use is multilevel so the variable should be equal to "ML".
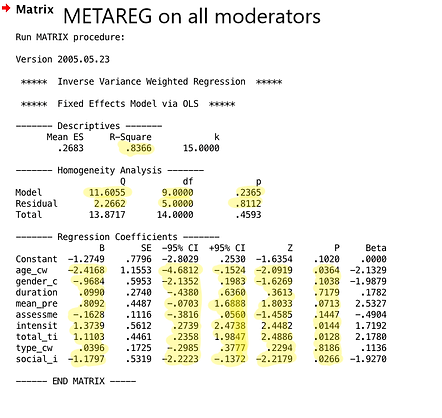
The Univariate Analysis macro gives you information about your individual moderators. The only value you need from this macro is the p value, which will tell you whether there is significant difference between the groups of a specific moderator. For example, if p < 0.05 for sex, that means the group containing only men has a significantly different effect size from the group of women only, as well as from the mixed sex group. These p values will eventually be entered into Table 2 in your publication. To get the p value for each moderator, run the MetaReg macro on each moderator's contrast weight variable separately. For example to get the p value for age, IVS should be equal to age_cw only. Below is an example of the output for age.

The Meta-Regression itself tells you which moderators account for a significant part of the variation among effect sizes. It is highly likely that you will find some studies with a significantly larger effect size than others. The beauty of a meta-analysis is that the meta-regression can help suggest potential causes for these larger or smaller effect sizes. You can also add something called an interaction into the overall meta-regression model. Interactions occur when the combination of two moderators explains more variability than either moderator alone. Interactions can be chosen based on theoretical data, or by looking at graphs created using MeanES. In order for the meta-regression to read the interaction, you must assign contrast weights to the various groups. For example, you could find that BMI and sex interact, meaning that obese men could have a significantly greater effect than normal men, and obese women may have a smaller effect than normal men but still a greater effect than normal weight women, etc.
To run the entire meta regression, change the IVS variable to be a list of all the moderator contrast weights. If your meta analysis does not have a lot of studies, you might get an error. If that happens it is probably because not enough cases overlap between certain moderators. Try playing around by taking some moderators out and doing different combinations while paying attention to "k", the number of cases being analyzed in the meta regression. Below is an example of an output with the important values highlighted.
NOTE: A moderator may be significant according to the meta-regression but not the univariate analysis and vise-versa. If this happens, do not despair!! Simply be prepared to offer some potential explanations for these findings and to look for interactions.






